jump to notes on Midterm II
jump to notes on Final Exam

In general, know

• how Taylor Series relates to techniques
• estimates of error
• comparison / tradeoffs between similar techniques
• what functions a technique is good for, what function it's bad for
• assumptions in order to use a technique (e.g. continuous function)
• affect of round-off error in various techniques

Topics

1. Math preliminaries
   • Reordering operations for efficiency: Horner's method
   • absolute & relative error
   • precision v. accuracy, significant digits
   • rounding, chopping

2. Taylor Series (TS)
   • TS equation - equality form and approximation form
   • TS expanded around a value, Maclaurin series
   • Mean value theorem as it relates to TS
   • truncated TS and error term: big-O notation
   • alternating series error term

3. Computer representations of numbers
   • base conversion
   • overflow, underflow, range
   • integer
   • fixed point
   • single precision
   • double precision
   • minimizing float point errors

4. Numerical Root Finding
   • Analysis & tradeoffs
     • Convergence, order of (linear, quadratic, superlinear)
     • Guaranteed convergence? under what conditions
     • Complexity of each step
     • Required input
   • closed (bracketed) approaches
     • Bisection method
     • Regula Falsi
   • open approaches
     • Newton's method
     • Secant method

5. Interpolation
   • interpolation v. approximation
   • noisy data - curve fitting - general idea
   • splines - piecewise curves - general idea
   • existence - by construction
   • Lagrange's form
   • Newton's form - divided differences (derivative information)
   • uniqueness property
   • Chebyshev nodes - what they are and general characteristics

6. Numerical Differentiation
   • first derivative using TS
   • order of error term (h^2, h^3, h^4, ...)
   • forward difference
   • backward difference
   • central difference
   • Richardson extrapolation - single application
   • Richardson extrapolation - m applications
   • second derivative using TS

7. Numerical Integration
   • Riemann integrable function
   • Trapezoidal Rule & error term
   • Composit Trapezoidal Rule
   • Recursive Trapezoidal Rule

Sample questions

Review homeworks

Some samples.

1. you're only interested in positive parameter values (x>0) and the function is monotonically increasing. How would you go about writing a program to find a root of an arbitrary monotonically increasing function?

2. For some function f(x),you have access to values f(0), f(0.5), f(1.0), f(1.5). f(2.0). Estimate its value at x= 0.75. Estimate its derivative at f(0.5). Estimate the integral from 0 to 2.0.

3. For some function f(x), you have access to values f(0), f'(0), and f''(0). How would you compute the derivative at x = 0.1? What is an upper bound on the error? What is the upper bound if you know that f'''(x) < 5 for 0
4. Given a monitonically increasing function that has monitonically increasing derivatives, what is the upper bound on using the following Taylor Series approximation to the function in the interval [0.0, 1.0]: f(0.25) ~ f(0) + f'(0)*0.25?

5. Construct a function that the Regula Falsi root finding algorithm would work well on, but bisection would not. Explain.

6. Given f(a), f(b), f(c), can you think of a way to compute the integral from a to b that is better than the Trapezoidal Rule? I'm looking for an idea here, not a specific formula.
7. Given the function graphed below and the information that there exists a root between 0 and 20, discuss how the various root finding algorithms would handle finding the root.

Same rules and format as with midterm #1 (see top of this page for a list)

In general know:

• Integration
• Linear Systems (see this note on solving a linear system)

TOPICS

• Integration
  • Trapezoid Rule
    • Single 2-point interval & error term
    • Composite form & error term
    • Recursive form
    • Romberg Integration (Richardson extrapolation) & error term
  • Simpson's Rules
    • single 3-point 1/3 interval & error term
    • single 4-point 3/8 interval & error term
    • Composite form & error term
  • Gaussian integration
  • Adaptive integration
  • Monte Carlo methods
    • random number generators, period, LCG
    • Monte Carlo integration (v. uniform sampling)
• Linear Systems
  • basics of linear systems of equations
  • forward elimination, back substitution
  • Matrices, properties, transpose, inverse, identity, determinant
  • matrix representation of linear systems
  • row, column operations on linear systems and corresponding matrix representation
  • LU decomposition and associated complexity

SAMPLE QUESTIONS

1. Given the function xxxx between 0 and 1, how well does the [Trapezoidal Rule using 1 inteval | 2-point Gaussian | ... ] compute the integral?
2. What is 'recursive trapezoid integration'?
3. What is adaptive integration?
4. How many Trapezoid intervals are necessary to approximate an integral within 0.1 if the derivatives are bounded by .2 in the interval?
5. Explain how to apply adaptive approach using Simpson's 1/3 rule.
6. What are the important properties of random number generators?
7. What is the period of an LCG?
8. How would you use Monte Carlo integration to compute the area inside an oval?
9. Given a system of linear equations,
   • put it in matrix form,
   • do forward elimination to convert A into an upper triangular matrix,
   • perform back substitution to solve for the unknowns
10. What is a permutation matrix and how does a given specific one affect a matrix?

Same rules and format as with midterms (see top of this page for a list)

Bascially, this course is about how to do math on a computer paying particular attention to:

• number representations, approximation, error terms, error bounds
• order of complexity, convergence, robustness
• code optimization (e.g. Horner's method, Gaussian elimination issues)

To prepare for the final:

• Review the midterms and homeworks
• Also review the notes for the 2 midterms.
• Review problems from the book.

Topics

• Preliminaries
  • Functions: continuity, derivative
  • bases & conversions, fractional numbers, float point, double precision, fixed point representations, round-off errors (rep & calc), precision, accuracy, absolute & relative error, chopping v. rounding, significant digits
  • Horner's method
  • Taylor series, functions: continuity, derivative, Mean Value theorem, alternating series

• Root finding (convergence, robustness)
  • factored form of functions
  • Open v. closed methods
  • Bisection, error, confergence
  • Regula Falsi
  • Newton's method, convergence rate
  • Secant

• Interpolation
  • Lagrange interpolation; Newton Form & divided differences, error term; uniqueness theorem, Chebyshev nodes
  • splines: cubic piecewise; advantages relative to Lagrange/Newton; matrix form P(u)=UMB; Hermite, Catmul-Rom, blended parabolas, Bezier, B-spline - just general idea of each; continuity between segments

• Differentiation (TS)
  • Taylor Series, truncation v. round-off errors
  • Forward difference
  • backward difference
  • central difference
  • Richardson extrapolation
  • 2nd derivative approximation

• Integration (error terms)
  • Reimann integrable function
  • Trapezoidal method: composite, recursive: error term
  • Romberg integration: order of error
  • Simpson's rule: 1/3, 3/8: error term
  • Gaussian quadrature: polynomial accuracy
  • Adaptive approaches
  • Monte Carlo integration, random number generators, LCG

• Systems of Equations
  • Matrix manipulations: addition, multiplication, scaling, associative v. commutative, identity, transpose, inverse, determinant, complexity of operations, special matrices: symmetric, diagonal, upper triangular, lower triangular, banded
  • Gaussian elimination: forward elimination, backward/forward substitution
  • Matrix representation, permutation matrix, LU decomposition, MAx = Ux = Mb, Ax = LUx
  • Pivoting, partial pivoting, scaled partial pivoting
  • Computing inverse: AX = I
  • Iterative methods: Jacobi, Gauss-Seidel, SOR - just the general idea, general form of the equation, and attributes of iterative methods. It's not necessary to know details of individual methods.

There will be questions on:

• Taylor series expansion and error term
• floating point format and round-off error
• Richardson extrapolation
• Scaled partial pivoting

See the sample questions from the midterms, above.

See the relevant sample exercises in the book (e.g., scaled partial pivoting)

1. Give pseudo code to efficiently calculate x^5 + x^3 + x, for some given variable x.
2. Give the three-term Taylor Series expansion of sin(x), where f'(x) = cos(x), f''(x) = -sin(x), f'''(x) = -cos(x), f''''(x) = sin(x). Also give a bound on the error.
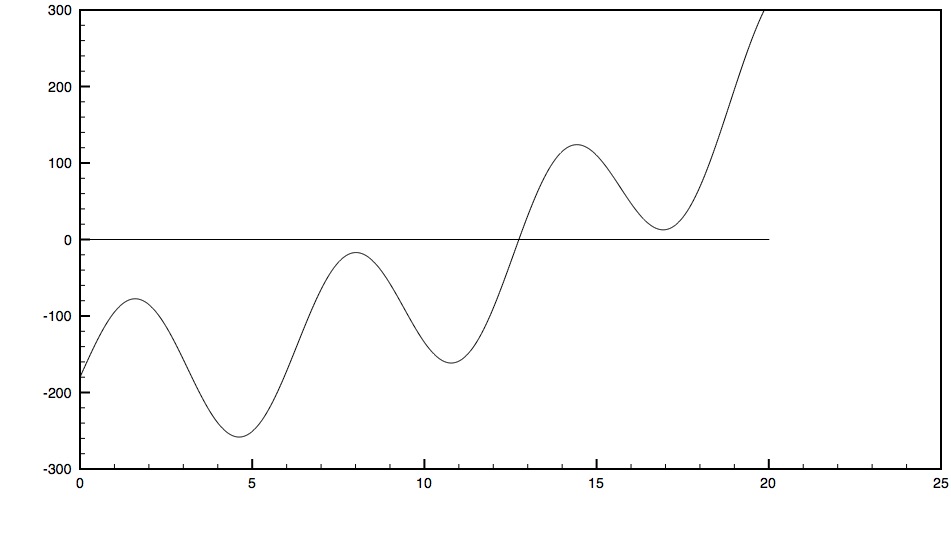
3. Show how the bisection method of root finding would work on the function graphed below.
4. Derive the central difference formula using Taylor Series expansion.
5. How is C-1 continuity enforced in Hermite splines?
6. What does AB=BA tell you about the matrices?
7. If A = LU, where L is a lower triangular matrix and U is an upper triangular matrix, explain how to solve Ax=b

Last updated 2/22/2012

CSE541 Class web page