
The software for all these four versions are available.
This book ``Curve and Surface Reconstruction: Algorithms with Mathematical Analysis" published by Canbridge U. Press contains the theory and algorithms for Cocone and related approaches.

We have also developed AMLS method for smoothing noisy point cloud data.
|
|
|
-
N. Amenta, S. Choi, T. K. Dey and N.
Leekha. A
simple algorithm for homeomorphic surface reconstruction. Proc. 16th Sympos. Comput. Geom., 2000,
213--222.

|
|
|
|
|
|
|
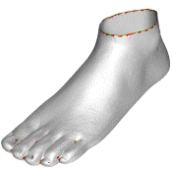
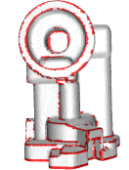
![]() Detection of Undersampling
Detection of Undersampling
-
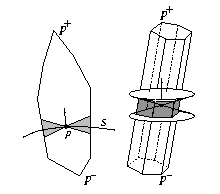
We detect undersampling from the samples.
Boundaries, regions of sharp edges, corners or high curvatures where undersampling
usually takes place are detected by this algorithm. This algorithm can be
used with crust or our cocone algorithm to make them robust and detect boundaries.
- There
is a new software Peel which may work better for detecting boundaries from
dense samples
|
|
|
|
|
|
|
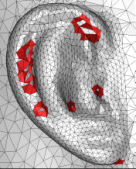
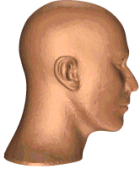
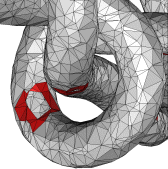
![]() Filling holes with Tight cocone
Filling holes with Tight cocone
-
After reconstruction with undersampling detection
we are sometimes left with small holes. We stitch these holes with Delaunay
triangles. We get almost `perfect' reconstruction in many cases. The details
appear in the following papers.
T. K. Dey and S. Goswami. Tight Cocone: A water-tight surface reconstructor. Journal of Computing and Information Science in Engineering, Vol. 3 (2003), 302--307.
|

|
|
|
|
|
|
|

|

|
|
|
|
|

|

|

|
|
for non-smooth edges) |
|
|
-
We extend the cocone algorithm to handle large
data in the range of million points. We avoid computing the Delaunay/Voronoi
diagram of the entire point set. Instead, we divide the data into chunks
using an octree subdivision and then apply cocone on each chunk. The matching
of surface pieces from adjacent octree cells are obtained by a `padding
mechanism' and some loacl properties of cocone. We have computed a surface
from a data of 3.5 million points in 3hrs 18 minutes with a PIII 733Mhz,
512MB,10GB PC.
T. K. Dey, J. Giesen and J. Hudson. Delaunay based shape reconstruction from large data. IEEE Symposium in Parallel and Large Data Visualization and Graphics, (2001), 19--27.
SuperCocone
code is available.
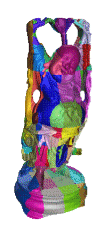
|
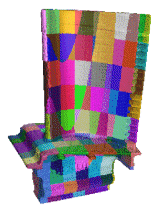
|
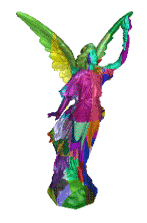
|
|
|
|
|
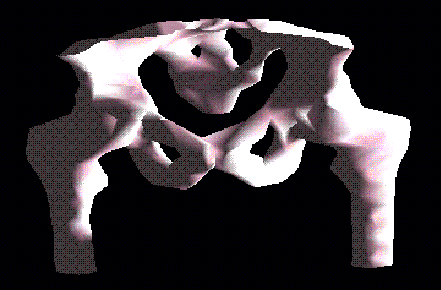
-
S. W. Cheng and T. K. Dey. Improved
construction of Delaunay based contour surfaces. Proc. ACM Sympos. Solid Modeling and Applications 99 1999,
322-323.
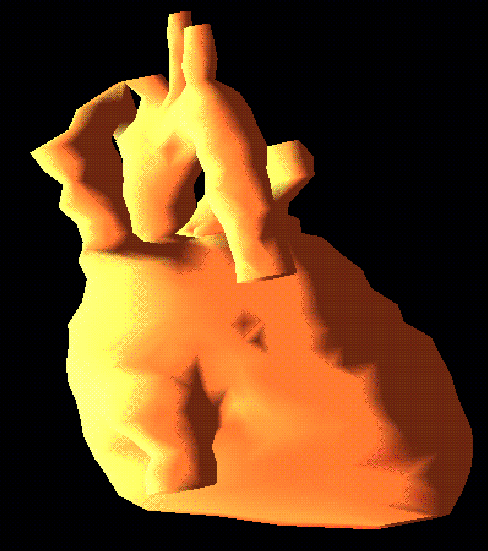
|
|
|
|
|
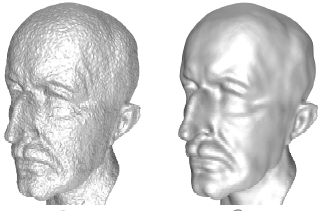
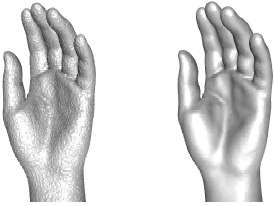
-
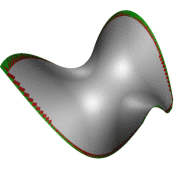
We use an implicit surface for point cloud data
smoothing. The moving least squares, MLS in short, are known for smoothing
point cloud data. We take a simple form of MLS and modify it to adapt to the
feature sizes of the sampled surface. We call it the adaptive MLS or AMLS
in short. The projection onto AMLS is achieved by Newton iterations which
is faster than the usual MLS projections. Further, it has other advantages
over the standard MLS.
T. K. Dey and J. Sun.
An
Adaptive MLS Surface for Reconstruction with Guarantees. IEEE Symposium on Geometry Processing, (2005), 43--52.
AMLS code is available.
|
|
|
|
|