|
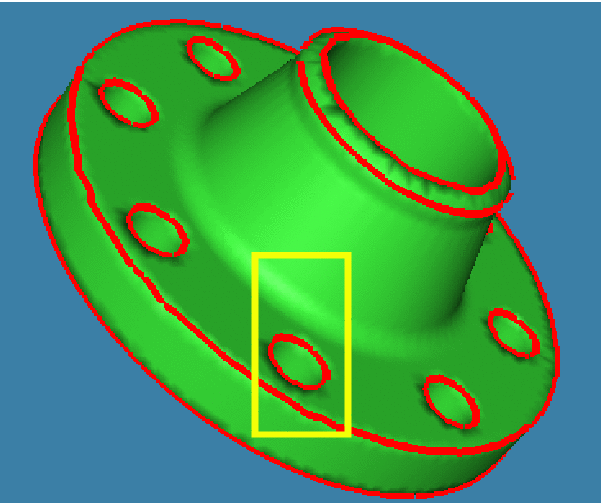
Constructing Isosurfaces with Sharp Edges and Corners using Cube Merging
A, Bhattacharya and R. Wenger.
Computer Graphics Forum, 32, 2013, 11-20.
A number of papers present algorithms to construct isosurfaces with
sharp edges and corners from hermite data, i.e. the exact surface
normals at the exact intersection
of the surface and grid edges. We discuss some fundamental problems
with the previous algorithms and describe a new approach, based on
merging grid cubes near sharp edges, that produces significantly better
results. Our algorithm requires only gradients at the grid vertices,
not at each surface-edge intersection point. We also give a method for
measuring the correctness of the resulting sharp edges and corners in
the isosurface.
Paper (pdf format)
Related tech report: Experimental Results on MergeSharp (pdf format)
|
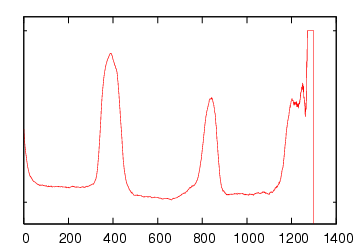
| On the Fractal Dimension of Isosurfaces
M. Khoury and R. Wenger.
IEEE Transactions on Visualization and Computer Graphics, 16, 2010, 1198-1205.
The fractal
dimension of an isosurface represents the growth in the isosurface as
the number of
grid cubes increases. We define and discuss the fractal isosurface
dimension, present statistics on the average fractal dimension of 60
publicly available benchmark data sets, show the fractal dimension is
highly correlated with topological noise in the benchmark data sets,
and present a formula predicting the fractal dimension as a function of
noise.
Paper(pdf format) |
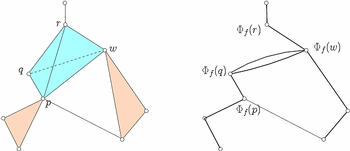 |
A Randomized O(m log m) Time Algorithm for Computing Reeb Graphs of Arbitrary Simplicial Complexes
W. Harvey, Y. Wang. and R. Wenger.
Proc. of the ACM Symposium on Computational Geometry (SOCG) 2010.
We present the first
sub-quadratic algorithm to compute the Reeb graph for a function on an
arbitrary simplicial complex K. Our algorithm is randomized with
an expected running time O(m log n) where m is the size of the
2-skeleton of K and n is the number of vertices. Our algorithm is
very simple to implement.
Paper(pdf format) |
 |
Isotopic
Reconstruction of Surfaces with Boundaries
T. K. Dey, K. Li., E. A. Ramos, and R. Wenger.
Proc. Sympos. Geom. Processing.(SGP09),
special issue of Computer Graphics Forum, Vol. 28, No. 5 (2009), 1371-1382.
[Web-page]
[Software]
We present an algorithm for
the reconstruction of a surface with boundaries (including a non-orientable
one) in three dimensions from a sufficiently dense sample. It is guaranteed
that the output is isotopic to the unknown sampled surface. No previously
known algorithm guarantees isotopic or homeomorphic reconstruction of surfaces
with boundaries. Our algorithm is surprisingly simple. It `peels' slivers
greedily from an alpha-complex of a sample of the surface. No other post-processing
is necessary. We provide several experimental results from an implementation
of our basic algorithm and also a modified version of it.
Paper (pdf format) |
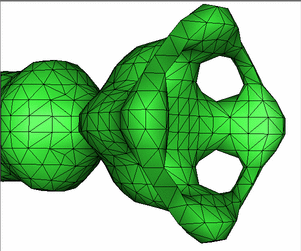
|
Quality Isosurface Mesh Generation Using an Extended
Marching Cubes Lookup Table
Sundaresan Raman and Rephael Wenger.
Computer Graphics Forum, 27, 2008, 791-798.
Abstract: The
Marching Cubes Algorithm may return degenerate, zero area isosurface
triangles, and often returns isosurface triangles with small areas,
edges or angles. We show how to avoid both problems using an extended
Marching Cubes lookup table. As opposed to the conventional Marching
Cubes lookup table, the extended lookup table differentiates scalar
values equal to the isovalue from scalar values greater than the
isovalue. The lookup table has 38 =
6561 entries, based on three possible labels, '-' or '=' or '+',
of each cube vertex. We present an algorithm based on this lookup table
which returns an isosurface close to the Marching Cubes isosurface, but
without any degenerate triangles or any small areas, edges or angles.
Paper (pdf format) |
 |
Isosurface Construction in Any Dimension Using Convex Hulls
Praveen Bhaniramka, Rephael Wenger and Roger Crawfis
IEEE Trans. on Visualization and Computer Graphics, 10, 2004, 353-400.
Abstract: We present an algorithm for constructing isosurfaces in
any dimension. The input to the algorithm is a set of scalar values in a d-dimensional regular grid of
(topological) hypercubes. The output is a set of (d-1)-dimensional simplices forming a piecewise linear approximation
to the isosurface. The algorithm
constructs the isosurface piecewise within each hypercube in the grid using the
convex hull of an appropriate set of points.
We prove that our algorithm correctly produces a triangulation of a (d-1)-manifold with boundary. In
dimensions three and four, lookup tables with 28 and 216
entries, respectively, can be used to speed the algorithm’s running time. In
three dimensions this gives the popular Marching Cubes algorithm. We discuss applications of four dimensional
isosurface construction to time varying isosurfaces, interval volumes and morphing.
Paper (pdf format)
|
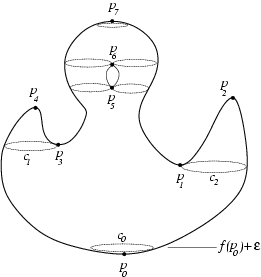 |
Stability of Critical Points with Interval Persistence
Tamal K. Dey and Rephael Wenger
Discrete and Computational Geometry, 38, 2007, 479-512.
Abstract: Scalar functions defined on a topological space W
are at the core of many applications such as shape matching,
visualization and physical simulations. Topological persistence is an
approach to characterizing these functions. It measures how long
topological structures in the sub-level sets {x in W: f(x) <=
c} persist as c changes. Recently it was shown that
the critical values defining a topological structure with
relatively large persistence remain almost unaffected by small
perturbations. This result suggests that topological persistence
is a good measure for matching and comparing scalar functions. We
extend these results to critical points in the domain by
redefining persistence and critical points and replacing sub-level
sets {x in W: f(x) <= c} with interval sets {x in W:
a <= f(x) < b}. With these modifications we establish a stability
result for critical points. This result is strengthened for maxima that
can be used for matching two scalar functions.
Paper (pdf format) |
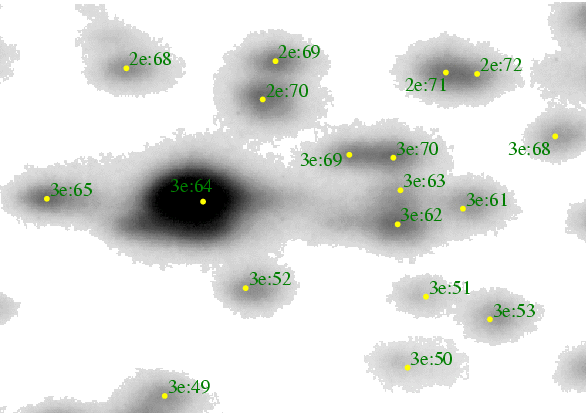 |
Contour Area Filtering of 2-Dimensional Electrophoresis Images
Ramakrishnan-Kazhiyur-Mannar, Dominic J Smiraglia, Christoph Plass and Rephael Wenger
Medical Image Analysis, 10, 2006, 353-365.
Abstract: We describe an algorithm, Contour Area Filtering, for separating
background from foreground in gray scale images. The algorithm is based on the area contained
within gray scale contour lines. It can
be viewed as a form of local thresholding, or as a seed growing algorithm, or
as a type of watershed segmentation. The
most important feature of the algorithm is that it uses object area to
determine the segmentation. Thus it is
relatively impervious to brightness and contrast variations across an image or
between different images.
Contour Area Filtering was designed specifically for image
analysis of 2D electrophoresis gels, although it can be applied to other gray
scale images...
Paper (pdf format)
|
 |
Restriction Landmark Genomic Scanning (RLGS) spot
identification by second generation virtual RLGS in multiple genomes
with multiple enzyme combinations
Authors: Dominic Smiraglia, Ramakrishnan
Kazhiyur-Mannar, Christopher Oakes, Yue-Zhong Wu, Ping Liang, Tahmina
Ansari, Jian Su, Laura Rush, Laura Smith, Li Yu, Chunhui Liu, Zunyan
Dai, Shih-Shih Chen, Shu-Huei Wang, Joseph Costello, Ilya Ioshikhes,
David Dawson, Jason Hong, Michael Teitell, Angela Szafranek, Marta
Camoriano, Fei Song, Rosemary Elliott, William Held, Jacquetta Trasler,
Christoph Plass and Rephael Wenger
BMC Genomics, 8:446, November 2007
Abstract: ... We report the development of a virtual RLGS method (vRLGS)
that allows for RLGS spot identification in any sequenced genome and with any
enzyme combination. We report
significant improvements in predicting DNA fragment migration patterns by
incorporating sequence information into the migration models, and demonstrate a
median Euclidian distance between actual and predicted spot migration of 0.18
centimeters for the most complex human RLGS pattern. We report the confirmed
identification of 795 human and 530 mouse RLGS spots for the most commonly used
enzyme combinations. We also developed a
method to filter the virtual spots to reduce the number of extra spots seen on
a virtual profile for both the mouse and human genomes. We demonstrate use of this filter to simplify
spot cloning and to assist in the identification of spots exhibiting
tissue-specific methylation...
Paper (pdf format)
|
Other papers (selected):
- T.K. Dey and R. Wenger, "Fast
Reconstruction of curves with sharp corners," Int. J. of Comp.
Geom. and Applications, 12 2002, pp. 353-400.
- J. Pach and R. Wenger, "Embedding
planar graphs at fixed vertex locations," Graphs and Combinatorics,
17 2001, pp. 717-728.
- P. Bhaniramka, R. Wenger and R. Crawfis, "Isosurfacing
in higher dimensions", Visualization 2000, Salt Lake City, Utah:
IEEE
Computer Society Press.
- T. Dey and R. Wenger, "Reconstructing
curves
with sharp corners", ACM Symp. on Computational Geometry, 2000.
- R. Wenger, "Progress in geometric
transversal
theory",
Contemporary Mathematics, B. Chazelle and J.E. Goodman, Eds., American
Math Society, 1999, pp. 375-393.
- H. Gupta and R. Wenger, "Constructing
piecewise linear homeomorphisms of simple polygons", J.
Algorithms, 22, 1997, pp. 142-157.
|









