
People
Research
Publications
(i) infer the one dimensional homology of a manifold from a very lean subsample,
(ii) reconstruct a surface in three dimension from a sparse subsample without computing Delaunay triangulations,
(iii) infer the persistent homology groups of compact sets from a sufficiently dense sample.
These results were published in the following paper:
[DFW13] T. K. Dey, F. Fan, and Y. Wang. Graph Induced Complex on Point Data. Proc. 29th Annu. Sympos. Comput. Geom. (2013).
GIComplex software based on the [DFW13] is available.
This project is supported by NSF grants CCF 1318595, CCF 1319406, CCF 1116258
 Construction
of the graph induced complex
Construction
of the graph induced complex
The following figures
illustrate the definition of the graph induced complex. |
 |
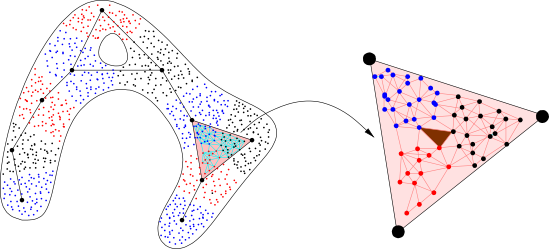 |
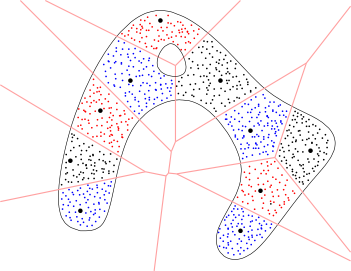
| Let (P,d) be a point set with a metric d and G(P) be a graph on P. | Let Q be a subset of P. Each point in P is mapped to its closest point in Q which is illustrated by the Voronoi diagram of Q. | The graph induced complex is constructed by collecting all simplices {q1, q2, ..., qk+1} if there is a (k+1)-clique in the graph G(P) with vertices {p1, p2, ..., pk+1} such that pi has qi (i=1,...,k+1) as its closest point in Q. |
 H1
inference from a very sparse subsample
H1
inference from a very sparse subsample
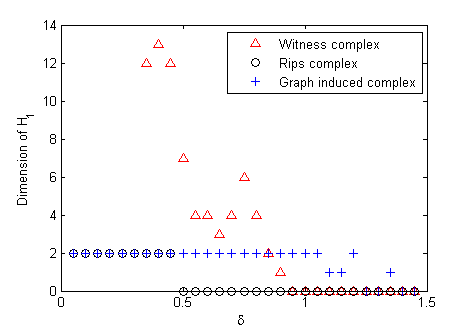
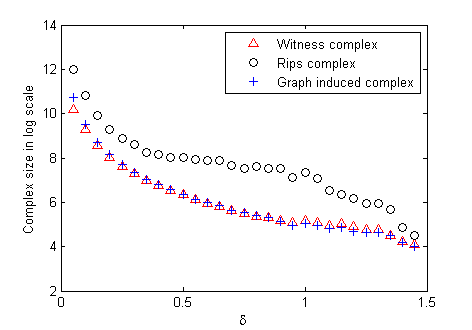
Using the concept of homological loop feature size (see [DFW13]), the graph induced complex can be very small but still capture the H1. In the Klein bottle example, there are 40,000 points sampled in R4. But the graph induced complex with size of 152 can still capture the H1 of the Klein bottle. The following two figures give the comparison results between graph induced complex and another two popular simplicial complexes: Rips and witness complexes for this example. The descriptions of these figures are referred to the paper [DFW13].
 |
 |
|
This figure compares the ability of the simplicial complex to capture the H1. |
This figure compares the size of the simplicial complex. |
 Surface
reconstruction by graph induced complex
Surface
reconstruction by graph induced complex
Using graph induced complex, a sparse triangular mesh can be reconstructed from a very dense input point set sampled from a surface in 3D. The following two examples both have dense input point sets P with |P| > 1,000,000. The reconstructed meshes have size in thousands (see the size information in the paper [DFW13]).
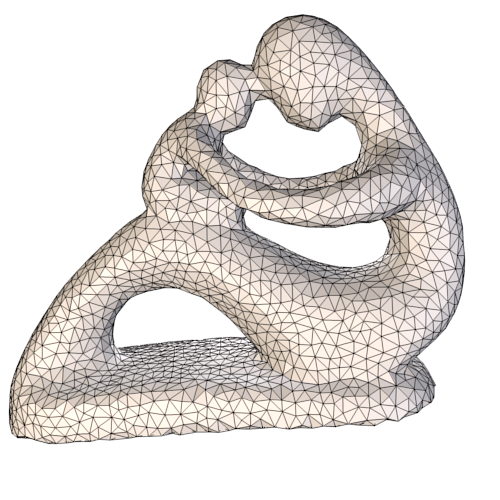 |
 |
| Reconstructed meshes by using graph induced complex | |