IJK: Isosurface Jeneration Kode

IJK is a set of C++ classes, routines and programs for generating isosurface. It includes programs for generating isosurface lookup tables for arbitrary convex polyhedra in arbitrary dimensions. It contains an implementation of the Marching Cubes Algorithm, the 4D Marching Cubes Algorithm, the Marching Cubes Algorithm using negative, equals and positive lookup tables, SnapMC which produces quality isosurface triangles, SHREC for constructing isosurfaces with sharp features using dual contouring and Religrad for computing reliable gradients from scalar data.  It also contains programs for reporting scalar data set information, for generating regular grid samplings of scalar and gradient fields, for measuring the angle distance between two surfaces, and for finding sharp edges in a mesh.

References:

Downloadable ijk software/tables:

Old versions of the software, isosurface tables and documentation.

Downloadable isosurface sharp feature reconstruction software:

Documentation:

Time-varying data:

Time varying volumetric data can be visualized by treating time as the fourth dimension and building a three-dimensional isosurface in 4D.  The isosurface can be sliced along the time axis to construct a time-varying animation or it can be sliced along other axes to visualize how subsets of the data vary in time.  For 10 time steps of the Jet ShockWave data set, an isovalue of 37 generated an isosurface with 8,021,739 tetrahedra and 1,394,104 vertices in 1109 seconds on an SGI Octane.  The isosurface intersected 1,317,975 hypercubes, giving an average of around 6 tetrahedra per hypercube.  The total number of triangles generated for the same 10 time steps by Marching Cubes was 1,796,350.
Slice along X-axis
Slice along Y-axis
Slice along Z-axis

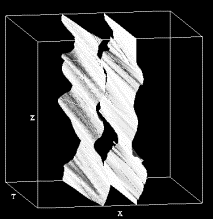
Slices of time-varying isosurface for the Jet Shockwave data set along different axes.

Isovalue = 37, Timesteps = 56-65.

Isosurface Morphing:

An isosurface in 3D can be morphed into another isosurface in 3D by constructing an appropriate isosurface in 4D.  Let f1(x,y,z) = 0 and f2(x,y,z)  = 0 define two isosurfaces, S1 and S2, respectively.  Define F(x,y,z,t) = f1(x,y,z)(1-t) + f2(x,y,z)t.  Note that F(x,y,z,0) = f1(x,y,z) and F(x,y,z,1) = f2(x,y,z).  Sample F along a four dimensional grid G(x,y,z,t) whose last value t is either 0 or 1.  Build an isosurface from the grid G and slice for various values of t to get a time-varying animation of the morph from S1 to S2.

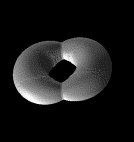
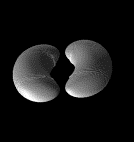
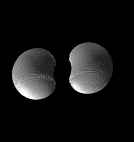
Morphing using isosurfaces in 4D.

Interval Volumes

An interval volume is the set of points lying between two isosufaces.  Three dimensional interval volumes can be constructed using a four dimensional isosurface.   Let f(x,y,z) = a1 and f(x,y,z) = a2 define two isosurfaces, S1 and S2, respectively.  Define F(x,y,z,w) = (f(x,y,z) - a1)(1-w) + (f(x,y,z) - a2)w.  Note that the isosurface F(x,y,z,0) = 0 equals S1 and the isosurface F(x,y,z,1) = 0 is S2.  Sample F along a four dimensional grid G(x,y,z,w) whose last value w is either 0 or 1. Build the isosurface with isovalue 0 from the grid G and project the tetrahedra into the plane  w = 0 to form the interval volume S1 and S2.
Interval volume
Wireframe

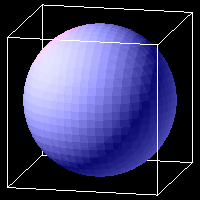
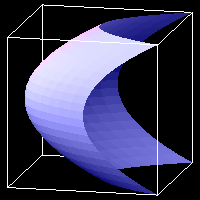
Interval volume for the sphere function constructed using 4D isosurfaces.

Visualizing functions:

A surface given by the equation F(x1, x2, ..., xd) = 0 can be visualized by evaluating F at the vertices of a d-dimensional grid, building an isosurface from that grid, and then slicing the isosurface by three-dimensional subspaces.
Slice along W-axis
Slice along X-axis
Slices of the function F(x,y,z,w) = x2+y2+z2-w along different coordinate axes.
Last updated by Dr. Rephael Wenger, Jan. 25, 2023